Standard Form Parabola Vertex . Another important point is the vertex or turning. If \(p>0\), the parabola opens up. The vertex form of a parabola's equation is generally expressed as: The standard form of a parabola is y=ax^2++bx+c, where a!=0. A parabola is defined as the locus (or collection) of points equidistant from a given point (the focus) and a given line (the directrix). (h, k) is the vertex. Thus, h is equal to negative b divided by 2 times a, and k is equal to c minus b squared divided by 4 times a. The vertex form of a parabola's equation is generally expressed as: If a is positive then the parabola opens upwards like a regular u. You can find the vertex given the standard form using the following formulas. The vertex is the minimum or maximum point of a parabola. Whenever we face a standard form of a parabola y = a·x² + b·x + c, we can use the equations of the vertex coordinates: Y = a(x − h)2 + k y = a (x − h) 2 + k.
from www.chegg.com
You can find the vertex given the standard form using the following formulas. Thus, h is equal to negative b divided by 2 times a, and k is equal to c minus b squared divided by 4 times a. If \(p>0\), the parabola opens up. A parabola is defined as the locus (or collection) of points equidistant from a given point (the focus) and a given line (the directrix). If a is positive then the parabola opens upwards like a regular u. The vertex form of a parabola's equation is generally expressed as: The standard form of a parabola is y=ax^2++bx+c, where a!=0. The vertex is the minimum or maximum point of a parabola. Whenever we face a standard form of a parabola y = a·x² + b·x + c, we can use the equations of the vertex coordinates: Y = a(x − h)2 + k y = a (x − h) 2 + k.
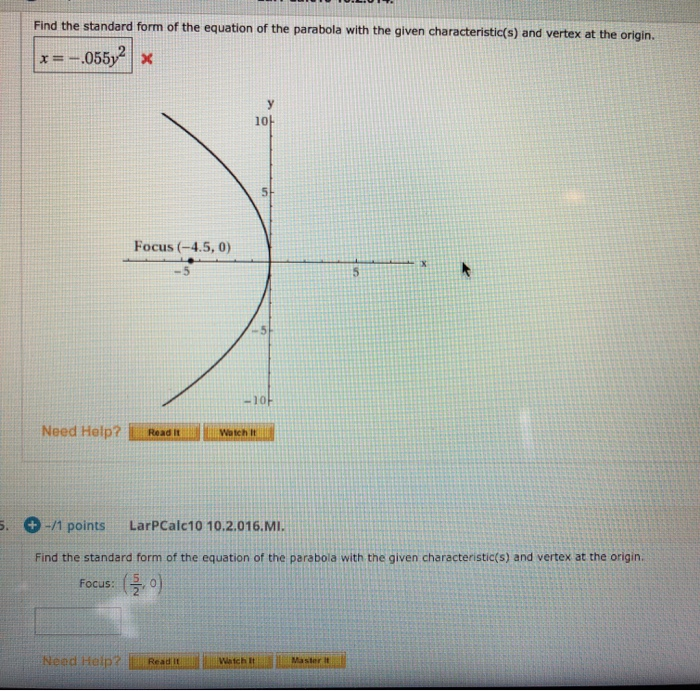
Solved Find the standard form of the equation of the
Standard Form Parabola Vertex A parabola is defined as the locus (or collection) of points equidistant from a given point (the focus) and a given line (the directrix). The vertex form of a parabola's equation is generally expressed as: (h, k) is the vertex. You can find the vertex given the standard form using the following formulas. The standard form of a parabola is y=ax^2++bx+c, where a!=0. Thus, h is equal to negative b divided by 2 times a, and k is equal to c minus b squared divided by 4 times a. Another important point is the vertex or turning. If a is positive then the parabola opens upwards like a regular u. The vertex is the minimum or maximum point of a parabola. Whenever we face a standard form of a parabola y = a·x² + b·x + c, we can use the equations of the vertex coordinates: The vertex form of a parabola's equation is generally expressed as: If \(p>0\), the parabola opens up. Y = a(x − h)2 + k y = a (x − h) 2 + k. A parabola is defined as the locus (or collection) of points equidistant from a given point (the focus) and a given line (the directrix).
From www.youtube.com
The Vertex Formula YouTube Standard Form Parabola Vertex Another important point is the vertex or turning. If a is positive then the parabola opens upwards like a regular u. If \(p>0\), the parabola opens up. Y = a(x − h)2 + k y = a (x − h) 2 + k. The standard form of a parabola is y=ax^2++bx+c, where a!=0. The vertex form of a parabola's equation. Standard Form Parabola Vertex.
From www.youtube.com
Graphing a Parabola from Standard Form YouTube Standard Form Parabola Vertex The standard form of a parabola is y=ax^2++bx+c, where a!=0. You can find the vertex given the standard form using the following formulas. Another important point is the vertex or turning. Y = a(x − h)2 + k y = a (x − h) 2 + k. (h, k) is the vertex. Whenever we face a standard form of a. Standard Form Parabola Vertex.
From www.animalia-life.club
Parabola Equation Standard Form Standard Form Parabola Vertex The vertex is the minimum or maximum point of a parabola. If a is positive then the parabola opens upwards like a regular u. The vertex form of a parabola's equation is generally expressed as: The vertex form of a parabola's equation is generally expressed as: The standard form of a parabola is y=ax^2++bx+c, where a!=0. If \(p>0\), the parabola. Standard Form Parabola Vertex.
From www.youtube.com
Day 7 HW 1 and 2 Convert the General Form Parabola to Vertex Form Standard Form Parabola Vertex The vertex form of a parabola's equation is generally expressed as: If \(p>0\), the parabola opens up. You can find the vertex given the standard form using the following formulas. The vertex form of a parabola's equation is generally expressed as: Another important point is the vertex or turning. Thus, h is equal to negative b divided by 2 times. Standard Form Parabola Vertex.
From www.cuemath.com
Vertex Formula Learn the Formula of Finding the Vertex of a Parabola Standard Form Parabola Vertex The vertex is the minimum or maximum point of a parabola. Thus, h is equal to negative b divided by 2 times a, and k is equal to c minus b squared divided by 4 times a. (h, k) is the vertex. Whenever we face a standard form of a parabola y = a·x² + b·x + c, we can. Standard Form Parabola Vertex.
From careerkeg.com
How To Write An Equation For A Parabola CAREER KEG Standard Form Parabola Vertex Y = a(x − h)2 + k y = a (x − h) 2 + k. Whenever we face a standard form of a parabola y = a·x² + b·x + c, we can use the equations of the vertex coordinates: The vertex form of a parabola's equation is generally expressed as: If \(p>0\), the parabola opens up. Thus, h. Standard Form Parabola Vertex.
From www.cuemath.com
Standard Form to Vertex Form Formula, Examples, FAQs Standard Form Parabola Vertex You can find the vertex given the standard form using the following formulas. A parabola is defined as the locus (or collection) of points equidistant from a given point (the focus) and a given line (the directrix). Thus, h is equal to negative b divided by 2 times a, and k is equal to c minus b squared divided by. Standard Form Parabola Vertex.
From www.slideserve.com
PPT Parabola PowerPoint Presentation, free download ID5580367 Standard Form Parabola Vertex A parabola is defined as the locus (or collection) of points equidistant from a given point (the focus) and a given line (the directrix). If a is positive then the parabola opens upwards like a regular u. The vertex form of a parabola's equation is generally expressed as: Thus, h is equal to negative b divided by 2 times a,. Standard Form Parabola Vertex.
From www.teachoo.com
Question 5 Family of parabolas having vertex at origin Standard Form Parabola Vertex If \(p>0\), the parabola opens up. The vertex form of a parabola's equation is generally expressed as: You can find the vertex given the standard form using the following formulas. Thus, h is equal to negative b divided by 2 times a, and k is equal to c minus b squared divided by 4 times a. Another important point is. Standard Form Parabola Vertex.
From www.vrogue.co
Parabolas Standard Form Vs Vertex Form Geogebra vrogue.co Standard Form Parabola Vertex (h, k) is the vertex. The standard form of a parabola is y=ax^2++bx+c, where a!=0. A parabola is defined as the locus (or collection) of points equidistant from a given point (the focus) and a given line (the directrix). If \(p>0\), the parabola opens up. Whenever we face a standard form of a parabola y = a·x² + b·x +. Standard Form Parabola Vertex.
From gradkastela.com
Standard Form Into Vertex Form Seven Things That Happen When You Are In Standard Form Parabola Vertex The vertex form of a parabola's equation is generally expressed as: If \(p>0\), the parabola opens up. Another important point is the vertex or turning. If a is positive then the parabola opens upwards like a regular u. The vertex form of a parabola's equation is generally expressed as: A parabola is defined as the locus (or collection) of points. Standard Form Parabola Vertex.
From www.protutorcompany.com
How to find vertex, focus, directrix of a parabola Standard Form Parabola Vertex Whenever we face a standard form of a parabola y = a·x² + b·x + c, we can use the equations of the vertex coordinates: If \(p>0\), the parabola opens up. Thus, h is equal to negative b divided by 2 times a, and k is equal to c minus b squared divided by 4 times a. The vertex form. Standard Form Parabola Vertex.
From www.ck12.org
Parabolas with Vertex at (h, k) CK12 Foundation Standard Form Parabola Vertex The vertex is the minimum or maximum point of a parabola. Another important point is the vertex or turning. Whenever we face a standard form of a parabola y = a·x² + b·x + c, we can use the equations of the vertex coordinates: A parabola is defined as the locus (or collection) of points equidistant from a given point. Standard Form Parabola Vertex.
From www.vrogue.co
Vertex Form How To Find The Equation Of A Parabola vrogue.co Standard Form Parabola Vertex Whenever we face a standard form of a parabola y = a·x² + b·x + c, we can use the equations of the vertex coordinates: Another important point is the vertex or turning. A parabola is defined as the locus (or collection) of points equidistant from a given point (the focus) and a given line (the directrix). (h, k) is. Standard Form Parabola Vertex.
From mrsnyderalgebra2.weebly.com
Quadratics Middle College Mathematics Lessons and Review Standard Form Parabola Vertex The vertex form of a parabola's equation is generally expressed as: Whenever we face a standard form of a parabola y = a·x² + b·x + c, we can use the equations of the vertex coordinates: If a is positive then the parabola opens upwards like a regular u. The standard form of a parabola is y=ax^2++bx+c, where a!=0. A. Standard Form Parabola Vertex.
From ar.inspiredpencil.com
Parabola Equation Standard Form Parabola Vertex Thus, h is equal to negative b divided by 2 times a, and k is equal to c minus b squared divided by 4 times a. The vertex form of a parabola's equation is generally expressed as: Whenever we face a standard form of a parabola y = a·x² + b·x + c, we can use the equations of the. Standard Form Parabola Vertex.
From www.numerade.com
SOLVED Write the standard form of the quadratic function whose graph Standard Form Parabola Vertex The vertex form of a parabola's equation is generally expressed as: A parabola is defined as the locus (or collection) of points equidistant from a given point (the focus) and a given line (the directrix). You can find the vertex given the standard form using the following formulas. Thus, h is equal to negative b divided by 2 times a,. Standard Form Parabola Vertex.
From www.youtube.com
09 Practice Graphing Parabolas Part 1 (Vertex Form & Standard Form Standard Form Parabola Vertex Y = a(x − h)2 + k y = a (x − h) 2 + k. Whenever we face a standard form of a parabola y = a·x² + b·x + c, we can use the equations of the vertex coordinates: If a is positive then the parabola opens upwards like a regular u. Thus, h is equal to negative. Standard Form Parabola Vertex.
From www.chegg.com
Solved Find the standard form of the equation of the Standard Form Parabola Vertex The vertex form of a parabola's equation is generally expressed as: If \(p>0\), the parabola opens up. The standard form of a parabola is y=ax^2++bx+c, where a!=0. (h, k) is the vertex. Another important point is the vertex or turning. The vertex form of a parabola's equation is generally expressed as: Y = a(x − h)2 + k y =. Standard Form Parabola Vertex.
From www.vrogue.co
Parabola Worksheet Math Aids vrogue.co Standard Form Parabola Vertex Y = a(x − h)2 + k y = a (x − h) 2 + k. Whenever we face a standard form of a parabola y = a·x² + b·x + c, we can use the equations of the vertex coordinates: The vertex form of a parabola's equation is generally expressed as: (h, k) is the vertex. The vertex is. Standard Form Parabola Vertex.
From mappingmemories.ca
Implementar Leve Color rosa vertex form calculator Descartar franja collar Standard Form Parabola Vertex Y = a(x − h)2 + k y = a (x − h) 2 + k. Whenever we face a standard form of a parabola y = a·x² + b·x + c, we can use the equations of the vertex coordinates: A parabola is defined as the locus (or collection) of points equidistant from a given point (the focus) and. Standard Form Parabola Vertex.
From brainly.com
The standard form for a parabola with vertex (h,k) and an axis of Standard Form Parabola Vertex The vertex form of a parabola's equation is generally expressed as: Thus, h is equal to negative b divided by 2 times a, and k is equal to c minus b squared divided by 4 times a. You can find the vertex given the standard form using the following formulas. If a is positive then the parabola opens upwards like. Standard Form Parabola Vertex.
From www.vrogue.co
Parabola Equation Properties Examples Parabola Formul vrogue.co Standard Form Parabola Vertex The vertex form of a parabola's equation is generally expressed as: If \(p>0\), the parabola opens up. You can find the vertex given the standard form using the following formulas. Whenever we face a standard form of a parabola y = a·x² + b·x + c, we can use the equations of the vertex coordinates: Thus, h is equal to. Standard Form Parabola Vertex.
From amulettejewelry.com
Graphing Parabolas In Vertex Form amulette Standard Form Parabola Vertex A parabola is defined as the locus (or collection) of points equidistant from a given point (the focus) and a given line (the directrix). Y = a(x − h)2 + k y = a (x − h) 2 + k. You can find the vertex given the standard form using the following formulas. The vertex form of a parabola's equation. Standard Form Parabola Vertex.
From montessorimuddle.org
Equations of a Parabola Standard to Vertex Form and Back Again Standard Form Parabola Vertex The vertex is the minimum or maximum point of a parabola. If a is positive then the parabola opens upwards like a regular u. Another important point is the vertex or turning. Thus, h is equal to negative b divided by 2 times a, and k is equal to c minus b squared divided by 4 times a. A parabola. Standard Form Parabola Vertex.
From www.ah-studio.com
Point Slope Form Parabola Why Is Point Slope Form Parabola So Famous Standard Form Parabola Vertex The standard form of a parabola is y=ax^2++bx+c, where a!=0. A parabola is defined as the locus (or collection) of points equidistant from a given point (the focus) and a given line (the directrix). (h, k) is the vertex. If \(p>0\), the parabola opens up. You can find the vertex given the standard form using the following formulas. Another important. Standard Form Parabola Vertex.
From courses.lumenlearning.com
The Parabola Algebra and Trigonometry Standard Form Parabola Vertex Thus, h is equal to negative b divided by 2 times a, and k is equal to c minus b squared divided by 4 times a. The vertex form of a parabola's equation is generally expressed as: The standard form of a parabola is y=ax^2++bx+c, where a!=0. The vertex is the minimum or maximum point of a parabola. Another important. Standard Form Parabola Vertex.
From elsenaju.eu
Vertex Form Calculator Standard Form Parabola Vertex Whenever we face a standard form of a parabola y = a·x² + b·x + c, we can use the equations of the vertex coordinates: If \(p>0\), the parabola opens up. Another important point is the vertex or turning. The vertex form of a parabola's equation is generally expressed as: You can find the vertex given the standard form using. Standard Form Parabola Vertex.
From brainly.com
The standard form for a parabola with vertex (h,k) and an axis of Standard Form Parabola Vertex If a is positive then the parabola opens upwards like a regular u. The vertex form of a parabola's equation is generally expressed as: A parabola is defined as the locus (or collection) of points equidistant from a given point (the focus) and a given line (the directrix). You can find the vertex given the standard form using the following. Standard Form Parabola Vertex.
From slidetodoc.com
4 2 STANDARD FORM OF A QUADRATIC FUNCTION Standard Form Parabola Vertex Whenever we face a standard form of a parabola y = a·x² + b·x + c, we can use the equations of the vertex coordinates: The vertex form of a parabola's equation is generally expressed as: If a is positive then the parabola opens upwards like a regular u. Y = a(x − h)2 + k y = a (x. Standard Form Parabola Vertex.
From owlcation.com
Parabola Equations and Graphs, Directrix and Focus and How to Find Standard Form Parabola Vertex The vertex form of a parabola's equation is generally expressed as: The vertex form of a parabola's equation is generally expressed as: The standard form of a parabola is y=ax^2++bx+c, where a!=0. (h, k) is the vertex. You can find the vertex given the standard form using the following formulas. A parabola is defined as the locus (or collection) of. Standard Form Parabola Vertex.
From study.com
Parabola in Standard Form Graphing, Rules & Examples Lesson Standard Form Parabola Vertex The standard form of a parabola is y=ax^2++bx+c, where a!=0. (h, k) is the vertex. If \(p>0\), the parabola opens up. You can find the vertex given the standard form using the following formulas. A parabola is defined as the locus (or collection) of points equidistant from a given point (the focus) and a given line (the directrix). If a. Standard Form Parabola Vertex.
From www.ck12.org
Parabolas with Vertex at the Origin CK12 Foundation Standard Form Parabola Vertex You can find the vertex given the standard form using the following formulas. Whenever we face a standard form of a parabola y = a·x² + b·x + c, we can use the equations of the vertex coordinates: The vertex form of a parabola's equation is generally expressed as: A parabola is defined as the locus (or collection) of points. Standard Form Parabola Vertex.
From www.youtube.com
How To Find The Vertex of a Parabola Standard Form, Factored & Vertex Standard Form Parabola Vertex If \(p>0\), the parabola opens up. The vertex form of a parabola's equation is generally expressed as: Another important point is the vertex or turning. Y = a(x − h)2 + k y = a (x − h) 2 + k. (h, k) is the vertex. Whenever we face a standard form of a parabola y = a·x² + b·x. Standard Form Parabola Vertex.
From www.animalia-life.club
Parabola Equation Standard Form Standard Form Parabola Vertex (h, k) is the vertex. The vertex is the minimum or maximum point of a parabola. Y = a(x − h)2 + k y = a (x − h) 2 + k. Whenever we face a standard form of a parabola y = a·x² + b·x + c, we can use the equations of the vertex coordinates: The vertex form. Standard Form Parabola Vertex.