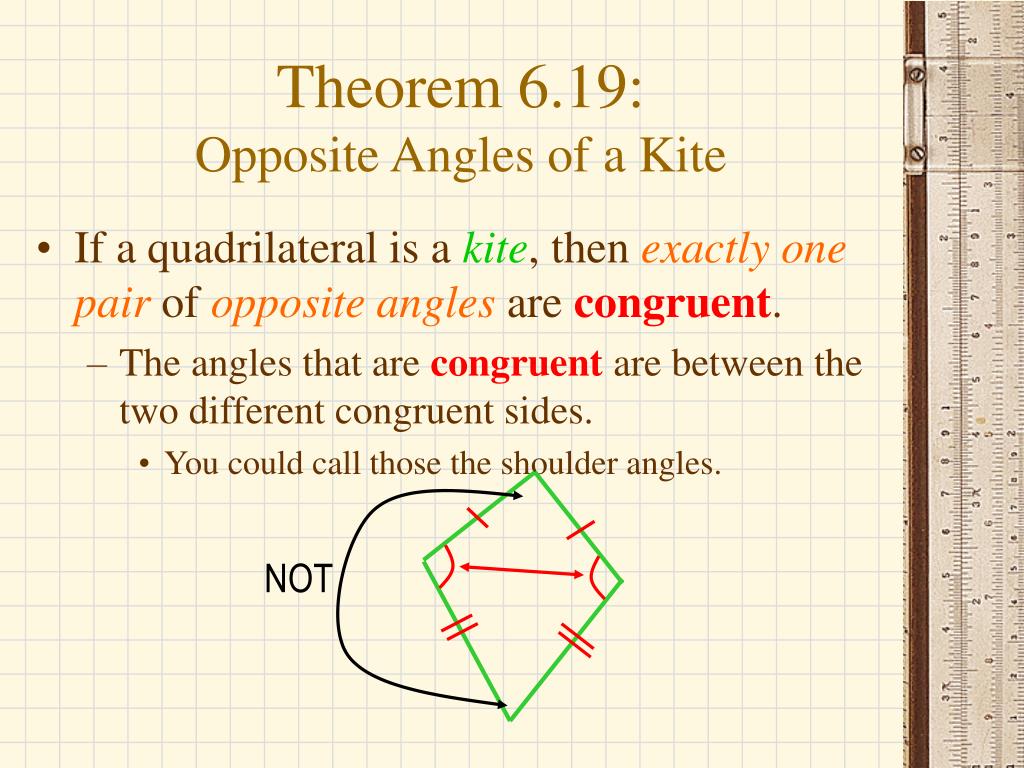
Kite Angle Theorem . (converse) if a trapezoid has its opposite angles supplementary, it is an isosceles trapezoid. There are many properties of kite geometry, but some of the most notable ones include the angle bisector theorem, the perpendicular bisector. The diagonals of a kite are perpendicular. The diagonals of a kite are perpendicular. Use the pythagorean theorem to find the length of the sides of the kite. Given a kite abcd with ab = ad and cb = cd, then triangle abc is congruent to triangle adc. This is an example that shows there is not. K e t and k i t are isosceles triangles , so e i ¯ is the perpendicular. A kite is a quadrilateral, a closed flat geometric shape in which two sets of neighboring or adjacent sides are congruent (equal in length). A kite is a quadrilateral whose four sides are drawn such that there are two distinct sets of. Figure \(\pageindex{5}\) \( \delta ket\) and \(\delta. Recall that the pythagorean theorem is a2 + b2 = c2, where c is the hypotenuse. In this kite, the sides are all. Here are two proofs that were found in class (my wording).
from www.slideserve.com
The diagonals of a kite are perpendicular. Figure \(\pageindex{5}\) \( \delta ket\) and \(\delta. Use the pythagorean theorem to find the length of the sides of the kite. A kite is a quadrilateral, a closed flat geometric shape in which two sets of neighboring or adjacent sides are congruent (equal in length). In this kite, the sides are all. The diagonals of a kite are perpendicular. A kite is a quadrilateral whose four sides are drawn such that there are two distinct sets of. Here are two proofs that were found in class (my wording). K e t and k i t are isosceles triangles , so e i ¯ is the perpendicular. Given a kite abcd with ab = ad and cb = cd, then triangle abc is congruent to triangle adc.
PPT Unit 6 PowerPoint Presentation, free download ID6751031
Kite Angle Theorem K e t and k i t are isosceles triangles , so e i ¯ is the perpendicular. Recall that the pythagorean theorem is a2 + b2 = c2, where c is the hypotenuse. Figure \(\pageindex{5}\) \( \delta ket\) and \(\delta. (converse) if a trapezoid has its opposite angles supplementary, it is an isosceles trapezoid. K e t and k i t are isosceles triangles , so e i ¯ is the perpendicular. A kite is a quadrilateral, a closed flat geometric shape in which two sets of neighboring or adjacent sides are congruent (equal in length). The diagonals of a kite are perpendicular. This is an example that shows there is not. Given a kite abcd with ab = ad and cb = cd, then triangle abc is congruent to triangle adc. Use the pythagorean theorem to find the length of the sides of the kite. There are many properties of kite geometry, but some of the most notable ones include the angle bisector theorem, the perpendicular bisector. Here are two proofs that were found in class (my wording). A kite is a quadrilateral whose four sides are drawn such that there are two distinct sets of. The diagonals of a kite are perpendicular. In this kite, the sides are all.
From study.com
Identifying Properties of Kites Geometry Kite Angle Theorem K e t and k i t are isosceles triangles , so e i ¯ is the perpendicular. This is an example that shows there is not. Here are two proofs that were found in class (my wording). There are many properties of kite geometry, but some of the most notable ones include the angle bisector theorem, the perpendicular bisector.. Kite Angle Theorem.
From dbdalrymplelethargy.z21.web.core.windows.net
Properties Of A Kite Geometry Kite Angle Theorem Use the pythagorean theorem to find the length of the sides of the kite. Here are two proofs that were found in class (my wording). This is an example that shows there is not. A kite is a quadrilateral, a closed flat geometric shape in which two sets of neighboring or adjacent sides are congruent (equal in length). K e. Kite Angle Theorem.
From goodttorials.blogspot.com
How To Find Missing Angles Of A Kite Kite Angle Theorem Recall that the pythagorean theorem is a2 + b2 = c2, where c is the hypotenuse. A kite is a quadrilateral whose four sides are drawn such that there are two distinct sets of. Given a kite abcd with ab = ad and cb = cd, then triangle abc is congruent to triangle adc. Figure \(\pageindex{5}\) \( \delta ket\) and. Kite Angle Theorem.
From www.cuemath.com
Properties of kite Definition of Kite with Solved Examples Cuemath Kite Angle Theorem A kite is a quadrilateral, a closed flat geometric shape in which two sets of neighboring or adjacent sides are congruent (equal in length). This is an example that shows there is not. Here are two proofs that were found in class (my wording). (converse) if a trapezoid has its opposite angles supplementary, it is an isosceles trapezoid. A kite. Kite Angle Theorem.
From www.youtube.com
Theorem of a Kite YouTube Kite Angle Theorem K e t and k i t are isosceles triangles , so e i ¯ is the perpendicular. This is an example that shows there is not. The diagonals of a kite are perpendicular. A kite is a quadrilateral, a closed flat geometric shape in which two sets of neighboring or adjacent sides are congruent (equal in length). There are. Kite Angle Theorem.
From www.geogebra.org
Quadrilateral kite theorem GeoGebra Kite Angle Theorem Use the pythagorean theorem to find the length of the sides of the kite. Here are two proofs that were found in class (my wording). A kite is a quadrilateral whose four sides are drawn such that there are two distinct sets of. The diagonals of a kite are perpendicular. A kite is a quadrilateral, a closed flat geometric shape. Kite Angle Theorem.
From www.cuemath.com
Properties of kite Definition of Kite with Solved Examples Cuemath Kite Angle Theorem There are many properties of kite geometry, but some of the most notable ones include the angle bisector theorem, the perpendicular bisector. K e t and k i t are isosceles triangles , so e i ¯ is the perpendicular. The diagonals of a kite are perpendicular. Figure \(\pageindex{5}\) \( \delta ket\) and \(\delta. In this kite, the sides are. Kite Angle Theorem.
From www.slideserve.com
PPT Assignment PowerPoint Presentation, free download ID2164666 Kite Angle Theorem A kite is a quadrilateral whose four sides are drawn such that there are two distinct sets of. The diagonals of a kite are perpendicular. Recall that the pythagorean theorem is a2 + b2 = c2, where c is the hypotenuse. A kite is a quadrilateral, a closed flat geometric shape in which two sets of neighboring or adjacent sides. Kite Angle Theorem.
From www.youtube.com
Proving a Quadrilateral Is a Kite Two Column Proofs Geometry YouTube Kite Angle Theorem K e t and k i t are isosceles triangles , so e i ¯ is the perpendicular. The diagonals of a kite are perpendicular. (converse) if a trapezoid has its opposite angles supplementary, it is an isosceles trapezoid. Use the pythagorean theorem to find the length of the sides of the kite. Figure \(\pageindex{5}\) \( \delta ket\) and \(\delta.. Kite Angle Theorem.
From www.youtube.com
Shape Properties Find Angle in Kite (Grade 3) OnMaths GCSE Maths Kite Angle Theorem A kite is a quadrilateral whose four sides are drawn such that there are two distinct sets of. In this kite, the sides are all. Figure \(\pageindex{5}\) \( \delta ket\) and \(\delta. Given a kite abcd with ab = ad and cb = cd, then triangle abc is congruent to triangle adc. The diagonals of a kite are perpendicular. This. Kite Angle Theorem.
From slideacceptance.blogspot.com
Properties Of A Kite Slide Acceptance Kite Angle Theorem A kite is a quadrilateral, a closed flat geometric shape in which two sets of neighboring or adjacent sides are congruent (equal in length). Recall that the pythagorean theorem is a2 + b2 = c2, where c is the hypotenuse. The diagonals of a kite are perpendicular. Use the pythagorean theorem to find the length of the sides of the. Kite Angle Theorem.
From www.slideserve.com
PPT 6.4 6.5 6.6 Quadrilaterals and Their Properties PowerPoint Kite Angle Theorem A kite is a quadrilateral whose four sides are drawn such that there are two distinct sets of. (converse) if a trapezoid has its opposite angles supplementary, it is an isosceles trapezoid. This is an example that shows there is not. Given a kite abcd with ab = ad and cb = cd, then triangle abc is congruent to triangle. Kite Angle Theorem.
From www.slideserve.com
PPT Properties of Trapezoids and Kites PowerPoint Presentation, free Kite Angle Theorem K e t and k i t are isosceles triangles , so e i ¯ is the perpendicular. A kite is a quadrilateral, a closed flat geometric shape in which two sets of neighboring or adjacent sides are congruent (equal in length). Given a kite abcd with ab = ad and cb = cd, then triangle abc is congruent to. Kite Angle Theorem.
From slideplayer.com
65 Trapezoids and Kites 2/15/17 ppt download Kite Angle Theorem Figure \(\pageindex{5}\) \( \delta ket\) and \(\delta. There are many properties of kite geometry, but some of the most notable ones include the angle bisector theorem, the perpendicular bisector. Given a kite abcd with ab = ad and cb = cd, then triangle abc is congruent to triangle adc. A kite is a quadrilateral whose four sides are drawn such. Kite Angle Theorem.
From www.cuemath.com
Properties of kite Definition of Kite with Solved Examples Cuemath Kite Angle Theorem Here are two proofs that were found in class (my wording). Given a kite abcd with ab = ad and cb = cd, then triangle abc is congruent to triangle adc. The diagonals of a kite are perpendicular. There are many properties of kite geometry, but some of the most notable ones include the angle bisector theorem, the perpendicular bisector.. Kite Angle Theorem.
From www.varsitytutors.com
How to find the length of the diagonal of a kite Advanced Geometry Kite Angle Theorem (converse) if a trapezoid has its opposite angles supplementary, it is an isosceles trapezoid. The diagonals of a kite are perpendicular. K e t and k i t are isosceles triangles , so e i ¯ is the perpendicular. Figure \(\pageindex{5}\) \( \delta ket\) and \(\delta. There are many properties of kite geometry, but some of the most notable ones. Kite Angle Theorem.
From ck12.org
Kites ( Read ) Geometry CK12 Foundation Kite Angle Theorem There are many properties of kite geometry, but some of the most notable ones include the angle bisector theorem, the perpendicular bisector. Here are two proofs that were found in class (my wording). This is an example that shows there is not. A kite is a quadrilateral whose four sides are drawn such that there are two distinct sets of.. Kite Angle Theorem.
From www.slideserve.com
PPT Trapezoids and Kites PowerPoint Presentation, free download ID Kite Angle Theorem A kite is a quadrilateral, a closed flat geometric shape in which two sets of neighboring or adjacent sides are congruent (equal in length). The diagonals of a kite are perpendicular. K e t and k i t are isosceles triangles , so e i ¯ is the perpendicular. Given a kite abcd with ab = ad and cb =. Kite Angle Theorem.
From www.ck12.org
Kites ( Read ) Geometry CK12 Foundation Kite Angle Theorem Figure \(\pageindex{5}\) \( \delta ket\) and \(\delta. In this kite, the sides are all. The diagonals of a kite are perpendicular. (converse) if a trapezoid has its opposite angles supplementary, it is an isosceles trapezoid. A kite is a quadrilateral whose four sides are drawn such that there are two distinct sets of. Use the pythagorean theorem to find the. Kite Angle Theorem.
From www.cuemath.com
Properties of a Kite Angles in a Kite, Kite Diagonals Kite Shape Kite Angle Theorem Figure \(\pageindex{5}\) \( \delta ket\) and \(\delta. K e t and k i t are isosceles triangles , so e i ¯ is the perpendicular. A kite is a quadrilateral whose four sides are drawn such that there are two distinct sets of. There are many properties of kite geometry, but some of the most notable ones include the angle. Kite Angle Theorem.
From klacqsvef.blob.core.windows.net
Kite Angles Acute at Alexandra Burris blog Kite Angle Theorem Given a kite abcd with ab = ad and cb = cd, then triangle abc is congruent to triangle adc. In this kite, the sides are all. Here are two proofs that were found in class (my wording). The diagonals of a kite are perpendicular. A kite is a quadrilateral whose four sides are drawn such that there are two. Kite Angle Theorem.
From www.slideserve.com
PPT Circle Theorems PowerPoint Presentation, free download ID3382753 Kite Angle Theorem This is an example that shows there is not. K e t and k i t are isosceles triangles , so e i ¯ is the perpendicular. (converse) if a trapezoid has its opposite angles supplementary, it is an isosceles trapezoid. Recall that the pythagorean theorem is a2 + b2 = c2, where c is the hypotenuse. Figure \(\pageindex{5}\) \(. Kite Angle Theorem.
From www.slideshare.net
8 5 Trapezoid And Kites Kite Angle Theorem K e t and k i t are isosceles triangles , so e i ¯ is the perpendicular. There are many properties of kite geometry, but some of the most notable ones include the angle bisector theorem, the perpendicular bisector. Recall that the pythagorean theorem is a2 + b2 = c2, where c is the hypotenuse. A kite is a. Kite Angle Theorem.
From www.slideserve.com
PPT The Circle PowerPoint Presentation, free download ID5239671 Kite Angle Theorem Use the pythagorean theorem to find the length of the sides of the kite. K e t and k i t are isosceles triangles , so e i ¯ is the perpendicular. Recall that the pythagorean theorem is a2 + b2 = c2, where c is the hypotenuse. (converse) if a trapezoid has its opposite angles supplementary, it is an. Kite Angle Theorem.
From www.youtube.com
Circles Circumscribed Angles (Kites) YouTube Kite Angle Theorem Here are two proofs that were found in class (my wording). The diagonals of a kite are perpendicular. K e t and k i t are isosceles triangles , so e i ¯ is the perpendicular. (converse) if a trapezoid has its opposite angles supplementary, it is an isosceles trapezoid. The diagonals of a kite are perpendicular. Use the pythagorean. Kite Angle Theorem.
From www.studocu.com
April 35 THEOREMS ON KITE MATHEMATICS GRADE 9 April 35, 2023 Name Kite Angle Theorem A kite is a quadrilateral, a closed flat geometric shape in which two sets of neighboring or adjacent sides are congruent (equal in length). This is an example that shows there is not. In this kite, the sides are all. Recall that the pythagorean theorem is a2 + b2 = c2, where c is the hypotenuse. The diagonals of a. Kite Angle Theorem.
From slideplayer.com
4.2 The Parallelogram and the Kite Theorems on Parallelograms ppt Kite Angle Theorem The diagonals of a kite are perpendicular. There are many properties of kite geometry, but some of the most notable ones include the angle bisector theorem, the perpendicular bisector. Here are two proofs that were found in class (my wording). The diagonals of a kite are perpendicular. A kite is a quadrilateral, a closed flat geometric shape in which two. Kite Angle Theorem.
From www.slideserve.com
PPT Assignment PowerPoint Presentation, free download ID2164666 Kite Angle Theorem This is an example that shows there is not. Recall that the pythagorean theorem is a2 + b2 = c2, where c is the hypotenuse. (converse) if a trapezoid has its opposite angles supplementary, it is an isosceles trapezoid. The diagonals of a kite are perpendicular. K e t and k i t are isosceles triangles , so e i. Kite Angle Theorem.
From study.com
Kite in Geometry Definition, Shape & Properties Lesson Kite Angle Theorem Given a kite abcd with ab = ad and cb = cd, then triangle abc is congruent to triangle adc. The diagonals of a kite are perpendicular. (converse) if a trapezoid has its opposite angles supplementary, it is an isosceles trapezoid. K e t and k i t are isosceles triangles , so e i ¯ is the perpendicular. A. Kite Angle Theorem.
From www.youtube.com
Determining the length of a kite using the pythagorean theorem YouTube Kite Angle Theorem Given a kite abcd with ab = ad and cb = cd, then triangle abc is congruent to triangle adc. (converse) if a trapezoid has its opposite angles supplementary, it is an isosceles trapezoid. Use the pythagorean theorem to find the length of the sides of the kite. Figure \(\pageindex{5}\) \( \delta ket\) and \(\delta. Recall that the pythagorean theorem. Kite Angle Theorem.
From www.slideserve.com
PPT Trapezoids and Kites PowerPoint Presentation, free download ID Kite Angle Theorem Figure \(\pageindex{5}\) \( \delta ket\) and \(\delta. A kite is a quadrilateral, a closed flat geometric shape in which two sets of neighboring or adjacent sides are congruent (equal in length). Recall that the pythagorean theorem is a2 + b2 = c2, where c is the hypotenuse. There are many properties of kite geometry, but some of the most notable. Kite Angle Theorem.
From www.slideserve.com
PPT Geometry B Bellwork PowerPoint Presentation, free download ID Kite Angle Theorem The diagonals of a kite are perpendicular. Use the pythagorean theorem to find the length of the sides of the kite. Recall that the pythagorean theorem is a2 + b2 = c2, where c is the hypotenuse. Here are two proofs that were found in class (my wording). (converse) if a trapezoid has its opposite angles supplementary, it is an. Kite Angle Theorem.
From www.slideserve.com
PPT Trapezoids and Kites PowerPoint Presentation, free download ID Kite Angle Theorem There are many properties of kite geometry, but some of the most notable ones include the angle bisector theorem, the perpendicular bisector. Given a kite abcd with ab = ad and cb = cd, then triangle abc is congruent to triangle adc. A kite is a quadrilateral whose four sides are drawn such that there are two distinct sets of.. Kite Angle Theorem.
From www.slideserve.com
PPT Unit 6 PowerPoint Presentation, free download ID6751031 Kite Angle Theorem Given a kite abcd with ab = ad and cb = cd, then triangle abc is congruent to triangle adc. The diagonals of a kite are perpendicular. K e t and k i t are isosceles triangles , so e i ¯ is the perpendicular. There are many properties of kite geometry, but some of the most notable ones include. Kite Angle Theorem.
From www.ck12.org
Kites ( Read ) Geometry CK12 Foundation Kite Angle Theorem Here are two proofs that were found in class (my wording). A kite is a quadrilateral, a closed flat geometric shape in which two sets of neighboring or adjacent sides are congruent (equal in length). The diagonals of a kite are perpendicular. In this kite, the sides are all. Use the pythagorean theorem to find the length of the sides. Kite Angle Theorem.