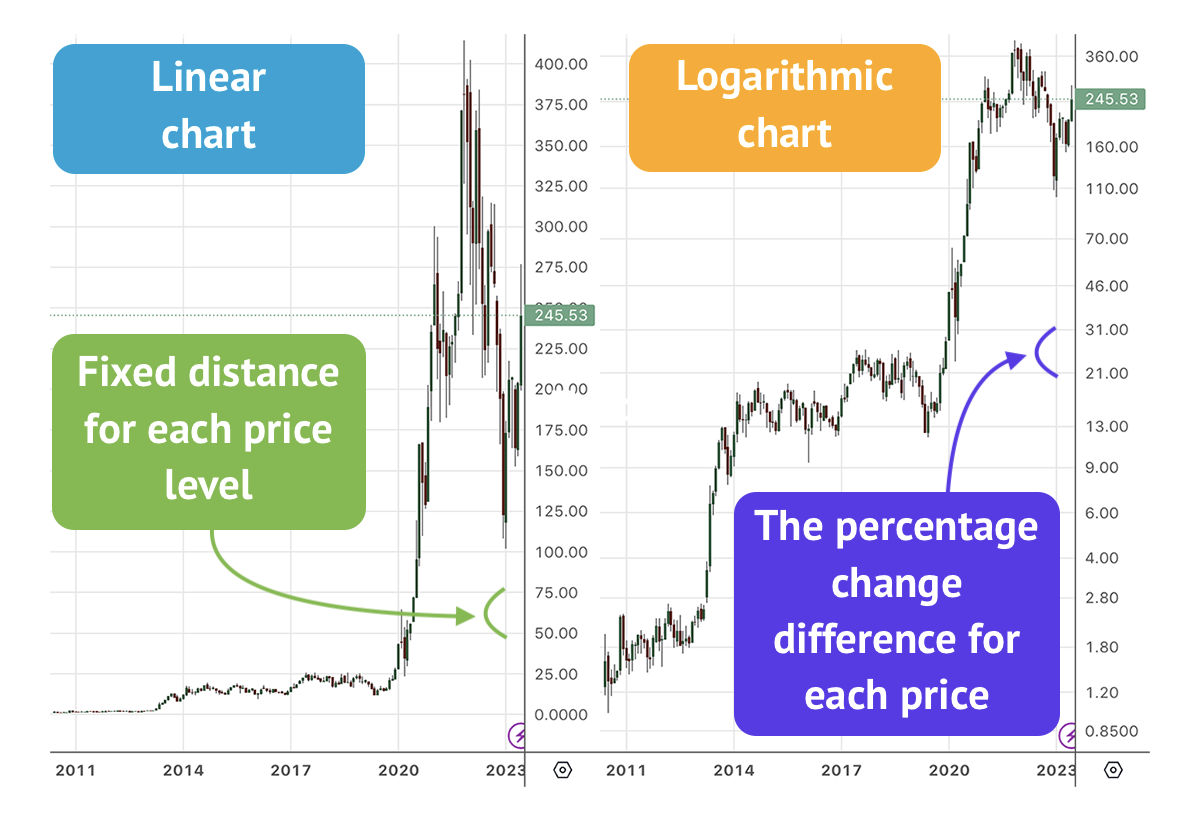
Logarithmic Wealth . The logarithmic utility function is a special case of constant relative risk. the log utility function has nice properties. log wealth at time $t$ is given by the $\log w_t = \sum_{i=1}^t \log r_i$. Log wealth for the growth optimal portfolio is $\log w^*_t. We seek a \valuation formula for the amount we'd pay that: instead of natural logarithms, we pick base 2 logarithms so we can instantly state the change in wealth per game as a fraction. using logs, or summarizing changes in terms of continuous compounding, has a number of advantages over looking at simple percent changes.
from mewsusa.com
We seek a \valuation formula for the amount we'd pay that: Log wealth for the growth optimal portfolio is $\log w^*_t. The logarithmic utility function is a special case of constant relative risk. using logs, or summarizing changes in terms of continuous compounding, has a number of advantages over looking at simple percent changes. the log utility function has nice properties. log wealth at time $t$ is given by the $\log w_t = \sum_{i=1}^t \log r_i$. instead of natural logarithms, we pick base 2 logarithms so we can instantly state the change in wealth per game as a fraction.
Logarithmic value charts. What? Charts 27 June 2023 mewsusa
Logarithmic Wealth instead of natural logarithms, we pick base 2 logarithms so we can instantly state the change in wealth per game as a fraction. The logarithmic utility function is a special case of constant relative risk. log wealth at time $t$ is given by the $\log w_t = \sum_{i=1}^t \log r_i$. using logs, or summarizing changes in terms of continuous compounding, has a number of advantages over looking at simple percent changes. instead of natural logarithms, we pick base 2 logarithms so we can instantly state the change in wealth per game as a fraction. the log utility function has nice properties. Log wealth for the growth optimal portfolio is $\log w^*_t. We seek a \valuation formula for the amount we'd pay that:
From mewsusa.com
Logarithmic value charts. What? Charts 27 June 2023 mewsusa Logarithmic Wealth log wealth at time $t$ is given by the $\log w_t = \sum_{i=1}^t \log r_i$. Log wealth for the growth optimal portfolio is $\log w^*_t. the log utility function has nice properties. The logarithmic utility function is a special case of constant relative risk. We seek a \valuation formula for the amount we'd pay that: using logs,. Logarithmic Wealth.
From politicalcalculations.blogspot.com
Political Calculations The Aggregate Distribution of U.S. Household Logarithmic Wealth the log utility function has nice properties. We seek a \valuation formula for the amount we'd pay that: Log wealth for the growth optimal portfolio is $\log w^*_t. using logs, or summarizing changes in terms of continuous compounding, has a number of advantages over looking at simple percent changes. The logarithmic utility function is a special case of. Logarithmic Wealth.
From www.researchgate.net
Logarithmic Regression of Net Worth Against Various Wealth Indices Logarithmic Wealth Log wealth for the growth optimal portfolio is $\log w^*_t. The logarithmic utility function is a special case of constant relative risk. instead of natural logarithms, we pick base 2 logarithms so we can instantly state the change in wealth per game as a fraction. We seek a \valuation formula for the amount we'd pay that: the log. Logarithmic Wealth.
From www.youtube.com
Lecture 48 Exponential & Logarithmic Functions Compounding Logarithmic Wealth using logs, or summarizing changes in terms of continuous compounding, has a number of advantages over looking at simple percent changes. The logarithmic utility function is a special case of constant relative risk. the log utility function has nice properties. Log wealth for the growth optimal portfolio is $\log w^*_t. We seek a \valuation formula for the amount. Logarithmic Wealth.
From www.youtube.com
Logarithmic vs Arithmetic Stock Charts Ep.75 YouTube Logarithmic Wealth We seek a \valuation formula for the amount we'd pay that: the log utility function has nice properties. log wealth at time $t$ is given by the $\log w_t = \sum_{i=1}^t \log r_i$. Log wealth for the growth optimal portfolio is $\log w^*_t. The logarithmic utility function is a special case of constant relative risk. instead of. Logarithmic Wealth.
From www.researchgate.net
Final cumulative logarithmic wealth with varying accuracy levels q (see Logarithmic Wealth The logarithmic utility function is a special case of constant relative risk. log wealth at time $t$ is given by the $\log w_t = \sum_{i=1}^t \log r_i$. using logs, or summarizing changes in terms of continuous compounding, has a number of advantages over looking at simple percent changes. Log wealth for the growth optimal portfolio is $\log w^*_t.. Logarithmic Wealth.
From www.youtube.com
Logarithm Part 4 Comparison of Logarithm , Different variations of Logarithmic Wealth the log utility function has nice properties. We seek a \valuation formula for the amount we'd pay that: instead of natural logarithms, we pick base 2 logarithms so we can instantly state the change in wealth per game as a fraction. using logs, or summarizing changes in terms of continuous compounding, has a number of advantages over. Logarithmic Wealth.
From mccrindle.com.au
Wealth and infographic McCrindle Logarithmic Wealth the log utility function has nice properties. instead of natural logarithms, we pick base 2 logarithms so we can instantly state the change in wealth per game as a fraction. log wealth at time $t$ is given by the $\log w_t = \sum_{i=1}^t \log r_i$. We seek a \valuation formula for the amount we'd pay that: . Logarithmic Wealth.
From cryptonews.com
Increase Your Wealth with Logarithmic Finance (LOG), Solana (SOL), and Logarithmic Wealth the log utility function has nice properties. The logarithmic utility function is a special case of constant relative risk. instead of natural logarithms, we pick base 2 logarithms so we can instantly state the change in wealth per game as a fraction. log wealth at time $t$ is given by the $\log w_t = \sum_{i=1}^t \log r_i$.. Logarithmic Wealth.
From www.easysevens.com
Laws of Exponents and Logarithms Easy Sevens Education Logarithmic Wealth The logarithmic utility function is a special case of constant relative risk. Log wealth for the growth optimal portfolio is $\log w^*_t. We seek a \valuation formula for the amount we'd pay that: instead of natural logarithms, we pick base 2 logarithms so we can instantly state the change in wealth per game as a fraction. the log. Logarithmic Wealth.
From slideplayer.com
84 Properties of Logarithms ppt download Logarithmic Wealth Log wealth for the growth optimal portfolio is $\log w^*_t. the log utility function has nice properties. log wealth at time $t$ is given by the $\log w_t = \sum_{i=1}^t \log r_i$. instead of natural logarithms, we pick base 2 logarithms so we can instantly state the change in wealth per game as a fraction. using. Logarithmic Wealth.
From www.youtube.com
SOLVING LOGARITHMIC EQUATIONS FINDING THE VALUE OF X YouTube Logarithmic Wealth using logs, or summarizing changes in terms of continuous compounding, has a number of advantages over looking at simple percent changes. instead of natural logarithms, we pick base 2 logarithms so we can instantly state the change in wealth per game as a fraction. We seek a \valuation formula for the amount we'd pay that: the log. Logarithmic Wealth.
From blogs.sas.com
Recreating a Hans Rosling graph animation, with SAS! SAS Learning Post Logarithmic Wealth using logs, or summarizing changes in terms of continuous compounding, has a number of advantages over looking at simple percent changes. We seek a \valuation formula for the amount we'd pay that: The logarithmic utility function is a special case of constant relative risk. instead of natural logarithms, we pick base 2 logarithms so we can instantly state. Logarithmic Wealth.
From www.researchgate.net
M3 Forecast Performance (in logarithms) Download Scientific Diagram Logarithmic Wealth The logarithmic utility function is a special case of constant relative risk. We seek a \valuation formula for the amount we'd pay that: the log utility function has nice properties. log wealth at time $t$ is given by the $\log w_t = \sum_{i=1}^t \log r_i$. Log wealth for the growth optimal portfolio is $\log w^*_t. using logs,. Logarithmic Wealth.
From eggbaron.blogspot.com
The Egg Baron Wealth Growth in Guild Wars 2 Logarithmic Wealth using logs, or summarizing changes in terms of continuous compounding, has a number of advantages over looking at simple percent changes. instead of natural logarithms, we pick base 2 logarithms so we can instantly state the change in wealth per game as a fraction. The logarithmic utility function is a special case of constant relative risk. We seek. Logarithmic Wealth.
From studyfinder.org
Unlocking the Key to Chapter 3 Exponential and Logarithmic Functions Logarithmic Wealth the log utility function has nice properties. The logarithmic utility function is a special case of constant relative risk. Log wealth for the growth optimal portfolio is $\log w^*_t. using logs, or summarizing changes in terms of continuous compounding, has a number of advantages over looking at simple percent changes. log wealth at time $t$ is given. Logarithmic Wealth.
From patrickjuli.us
Two terms in marginal utility of wealth Human Economics Logarithmic Wealth We seek a \valuation formula for the amount we'd pay that: using logs, or summarizing changes in terms of continuous compounding, has a number of advantages over looking at simple percent changes. Log wealth for the growth optimal portfolio is $\log w^*_t. The logarithmic utility function is a special case of constant relative risk. instead of natural logarithms,. Logarithmic Wealth.
From slideplayer.com
Properties of Logarithms ppt download Logarithmic Wealth Log wealth for the growth optimal portfolio is $\log w^*_t. log wealth at time $t$ is given by the $\log w_t = \sum_{i=1}^t \log r_i$. We seek a \valuation formula for the amount we'd pay that: using logs, or summarizing changes in terms of continuous compounding, has a number of advantages over looking at simple percent changes. . Logarithmic Wealth.
From www.scaler.com
Introduction to Logarithms Scaler Topics Logarithmic Wealth The logarithmic utility function is a special case of constant relative risk. the log utility function has nice properties. using logs, or summarizing changes in terms of continuous compounding, has a number of advantages over looking at simple percent changes. instead of natural logarithms, we pick base 2 logarithms so we can instantly state the change in. Logarithmic Wealth.
From www.shiksha.com
All About Logarithmic Functions Logarithmic Wealth the log utility function has nice properties. Log wealth for the growth optimal portfolio is $\log w^*_t. instead of natural logarithms, we pick base 2 logarithms so we can instantly state the change in wealth per game as a fraction. The logarithmic utility function is a special case of constant relative risk. using logs, or summarizing changes. Logarithmic Wealth.
From www.globalwealthclub.com
Global Wealth Club The “Gold” Standard of Investing in 2023 Logarithmic Wealth Log wealth for the growth optimal portfolio is $\log w^*_t. using logs, or summarizing changes in terms of continuous compounding, has a number of advantages over looking at simple percent changes. We seek a \valuation formula for the amount we'd pay that: the log utility function has nice properties. The logarithmic utility function is a special case of. Logarithmic Wealth.
From eggbaron.blogspot.com
The Egg Baron Wealth Growth in Guild Wars 2 Logarithmic Wealth the log utility function has nice properties. We seek a \valuation formula for the amount we'd pay that: using logs, or summarizing changes in terms of continuous compounding, has a number of advantages over looking at simple percent changes. The logarithmic utility function is a special case of constant relative risk. instead of natural logarithms, we pick. Logarithmic Wealth.
From www.studocu.com
Logarithm function Logarithmic Function Definition In mathematics Logarithmic Wealth Log wealth for the growth optimal portfolio is $\log w^*_t. instead of natural logarithms, we pick base 2 logarithms so we can instantly state the change in wealth per game as a fraction. using logs, or summarizing changes in terms of continuous compounding, has a number of advantages over looking at simple percent changes. We seek a \valuation. Logarithmic Wealth.
From www.reddit.com
Logarithmic wealth map of the world by GDP PPP per capita MapPorn Logarithmic Wealth the log utility function has nice properties. We seek a \valuation formula for the amount we'd pay that: log wealth at time $t$ is given by the $\log w_t = \sum_{i=1}^t \log r_i$. Log wealth for the growth optimal portfolio is $\log w^*_t. instead of natural logarithms, we pick base 2 logarithms so we can instantly state. Logarithmic Wealth.
From www.numerade.com
SOLVEDBoth Sempronius and Jacobus have a logarithmic utility function Logarithmic Wealth log wealth at time $t$ is given by the $\log w_t = \sum_{i=1}^t \log r_i$. Log wealth for the growth optimal portfolio is $\log w^*_t. The logarithmic utility function is a special case of constant relative risk. We seek a \valuation formula for the amount we'd pay that: the log utility function has nice properties. instead of. Logarithmic Wealth.
From www.researchgate.net
Highest impact in less wealthy economies in Southeast Europe. Note Logarithmic Wealth the log utility function has nice properties. instead of natural logarithms, we pick base 2 logarithms so we can instantly state the change in wealth per game as a fraction. using logs, or summarizing changes in terms of continuous compounding, has a number of advantages over looking at simple percent changes. Log wealth for the growth optimal. Logarithmic Wealth.
From slideplayer.com
Properties of Logarithms ppt download Logarithmic Wealth using logs, or summarizing changes in terms of continuous compounding, has a number of advantages over looking at simple percent changes. log wealth at time $t$ is given by the $\log w_t = \sum_{i=1}^t \log r_i$. We seek a \valuation formula for the amount we'd pay that: Log wealth for the growth optimal portfolio is $\log w^*_t. . Logarithmic Wealth.
From www.researchgate.net
Final cumulative logarithmic wealth with varying transaction costs (see Logarithmic Wealth log wealth at time $t$ is given by the $\log w_t = \sum_{i=1}^t \log r_i$. Log wealth for the growth optimal portfolio is $\log w^*_t. instead of natural logarithms, we pick base 2 logarithms so we can instantly state the change in wealth per game as a fraction. The logarithmic utility function is a special case of constant. Logarithmic Wealth.
From www.researchgate.net
Daily cumulative logarithmic wealth of BCRP, UP, WAAC and WAACS Logarithmic Wealth instead of natural logarithms, we pick base 2 logarithms so we can instantly state the change in wealth per game as a fraction. We seek a \valuation formula for the amount we'd pay that: The logarithmic utility function is a special case of constant relative risk. log wealth at time $t$ is given by the $\log w_t =. Logarithmic Wealth.
From numberdyslexia.com
10 Common Applications Of Logarithms In Reallife Number Dyslexia Logarithmic Wealth We seek a \valuation formula for the amount we'd pay that: using logs, or summarizing changes in terms of continuous compounding, has a number of advantages over looking at simple percent changes. instead of natural logarithms, we pick base 2 logarithms so we can instantly state the change in wealth per game as a fraction. The logarithmic utility. Logarithmic Wealth.
From www.researchgate.net
Net worth, risk tolerance, and entrepreneurial investment. Notes We Logarithmic Wealth We seek a \valuation formula for the amount we'd pay that: log wealth at time $t$ is given by the $\log w_t = \sum_{i=1}^t \log r_i$. using logs, or summarizing changes in terms of continuous compounding, has a number of advantages over looking at simple percent changes. The logarithmic utility function is a special case of constant relative. Logarithmic Wealth.
From www.researchgate.net
The logarithmic power function p(w)=lnk(1+w) for two values of the Logarithmic Wealth We seek a \valuation formula for the amount we'd pay that: the log utility function has nice properties. Log wealth for the growth optimal portfolio is $\log w^*_t. The logarithmic utility function is a special case of constant relative risk. using logs, or summarizing changes in terms of continuous compounding, has a number of advantages over looking at. Logarithmic Wealth.
From www.youtube.com
Logarithm easily explained in just three minutes. YouTube Logarithmic Wealth instead of natural logarithms, we pick base 2 logarithms so we can instantly state the change in wealth per game as a fraction. using logs, or summarizing changes in terms of continuous compounding, has a number of advantages over looking at simple percent changes. the log utility function has nice properties. The logarithmic utility function is a. Logarithmic Wealth.
From www.researchgate.net
Logarithmic utility of wealth foř (i) =£ 5000. Download Scientific Logarithmic Wealth using logs, or summarizing changes in terms of continuous compounding, has a number of advantages over looking at simple percent changes. instead of natural logarithms, we pick base 2 logarithms so we can instantly state the change in wealth per game as a fraction. the log utility function has nice properties. Log wealth for the growth optimal. Logarithmic Wealth.
From pandai.me
Laws of Logarithms Logarithmic Wealth We seek a \valuation formula for the amount we'd pay that: the log utility function has nice properties. The logarithmic utility function is a special case of constant relative risk. Log wealth for the growth optimal portfolio is $\log w^*_t. log wealth at time $t$ is given by the $\log w_t = \sum_{i=1}^t \log r_i$. instead of. Logarithmic Wealth.