k-Nearest Neighbors#

k-Nearest Neighbors is a nonparametric model. The idea is simple:

  • choose hyperparameter \(k\in\mathbb N\);

  • choose a distance metric in \(\mathbb R^d\) (for example, Euclidean);

  • for a sample \(\boldsymbol x \in \mathbb R^d\) find its \(k\) nearest neighbors among the training dataset;

  • classify or predict the label of \(\boldsymbol x\) according to the labels of its neighbors.

Distance in \(\mathbb R^d\)#

How to calculate distance \(\rho (\boldsymbol x, \boldsymbol y)\) of vectors \(\boldsymbol x, \boldsymbol y \in\mathbb R^d\)?

  • Euclidean distance: \(\rho_2(\boldsymbol x, \boldsymbol y) = \sqrt{\sum\limits_{i=1}^d (x_i - y_i)^2}\)

  • Manhattan distance: \(\rho_1(\boldsymbol x, \boldsymbol y) = \sum\limits_{i=1}^d |x_i - y_i|\)

  • Minkowski distance: \(\rho_p(\boldsymbol x, \boldsymbol y) = \Big(\sum\limits_{i=1}^d |x_i - y_i|^p \Big)^{\frac 1p}\), \(p \geqslant 1\)

Note

The distance to zero vector \(\rho_p(\boldsymbol x, \boldsymbol 0)\) is called \(p\)-norm:

\[ \| \boldsymbol x \|_p = \Big(\sum\limits_{i=1}^d |x_i|^p \Big)^{\frac 1p} \]

The unit ball in \(\mathbb R^d\) with respect to \(p\)-norm is defined as

\[ \{\boldsymbol x \in \mathbb R^d \colon \|\boldsymbol x\|_p \leqslant 1\}. \]
---------------------------------------------------------------------------
ModuleNotFoundError                       Traceback (most recent call last)
Cell In[1], line 2
      1 import numpy as np
----> 2 import plotly.graph_objects as go
      4 from matplotlib import cm
      5 from matplotlib.colors import ListedColormap, LinearSegmentedColormap, to_hex

ModuleNotFoundError: No module named 'plotly'

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[2], line 1
----> 1 plot_slider_minkowski([0.67, 0.8, 1, 1.2, 1.4, 1.5,  1.6, 1.8, 2, 2.2, 2.5, 3, 4, 5, 7, 10, "∞"], write_html=True)

NameError: name 'plot_slider_minkowski' is not defined

Q. The “infinite” norm is defined as

\[ \| \boldsymbol x \|_\infty = \lim\limits_{p\to +\infty} \| \boldsymbol x \|_p. \]

What is the value of \(\lim\limits_{p\to +\infty} \Big(\sum\limits_{i=1}^d |x_i|^p \Big)^{\frac 1p}\)?

k-NN algorithm#

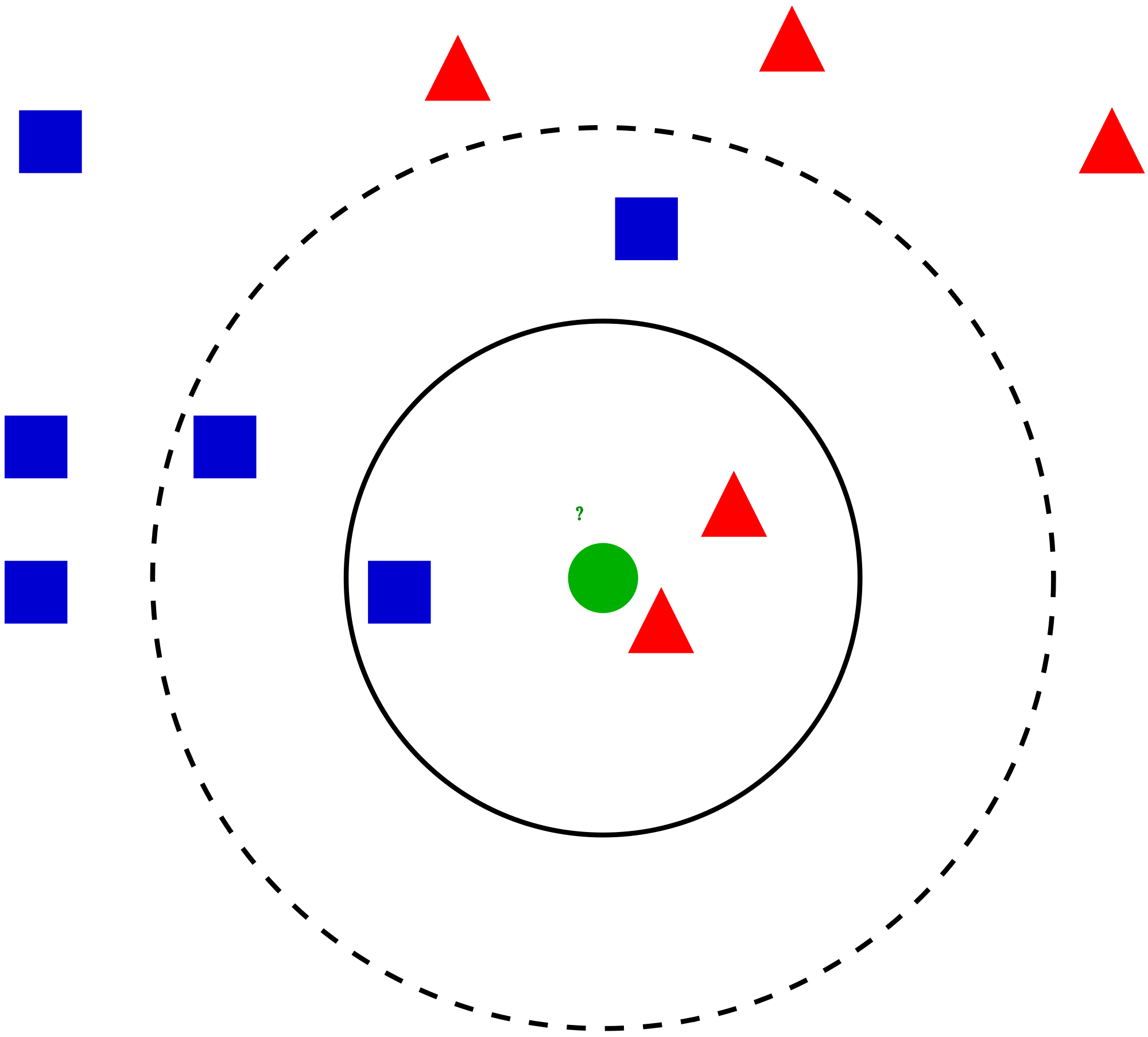
https://cdn.analyticsvidhya.com/wp-content/uploads/2018/03/knn3.png

Given the training dataset \(\{(\boldsymbol x_i, y_i)\}_{i=1}^n\), how to classify a new object \(\boldsymbol x\)?

  1. Sort distances \(\rho (\boldsymbol x_i, \boldsymbol x)\) in increasing order:

    \[ \rho (\boldsymbol x_{(1)}, \boldsymbol x) \leqslant \rho (\boldsymbol x_{(2)}, \boldsymbol x) \leqslant \ldots \leqslant \rho (\boldsymbol x_{(n)}, \boldsymbol x) \]

  2. So \(\boldsymbol x_{(i)}\) is the \(i\)-th neighbor of the object \(\boldsymbol x\)

  3. Let \(y_{(i)}\) be the label of \(\boldsymbol x_{(i)}\)

  4. The label \(\hat y\) of the object \(\boldsymbol x\in\mathbb R^d\) is set to the most common label among \(k\) neighbors of \(\boldsymbol x\):

\[ \widehat y = \arg\max_{y\in Y} \sum\limits_{i=1}^k [y = y_{(i)}] \]

For regression task the last step is subsituted by

\[ \widehat y = \frac 1k\sum\limits_{i=1}^k y_{(i)}. \]

Note that \(\widehat y = y_{(1)}\) if \(k=1\).

Voronoi tessellation#

A k-NN classifier with \(k=1\) induces a Voronoi tessellation of the points. This is a partition of space which associates a region \(V(\boldsymbol x_i)\) with each sample \(\boldsymbol x_i\) in such a way that all points in \(V(\boldsymbol x_i)\) are closer to \(\boldsymbol x_i\) than to any other point. In other words,

\[ V(\boldsymbol x_i) = \{\boldsymbol z \in \mathbb R^n\colon \rho(\boldsymbol x_i, \boldsymbol z) < \rho(\boldsymbol x_j, \boldsymbol z) \text{ for all }j\ne i\}. \]
../_images/6cdd3093bc6d74dfcd4d7fecd961e0a33ed3f8604b80eebadc15f100e4c81fae.svg

Role of \(k\)#

The decision boundaries become smoother as \(k\) grows. Here is an example from [Murphy, 2022] (figure 16.2): k-NN algorithm is applied to simulated data with three clusters.

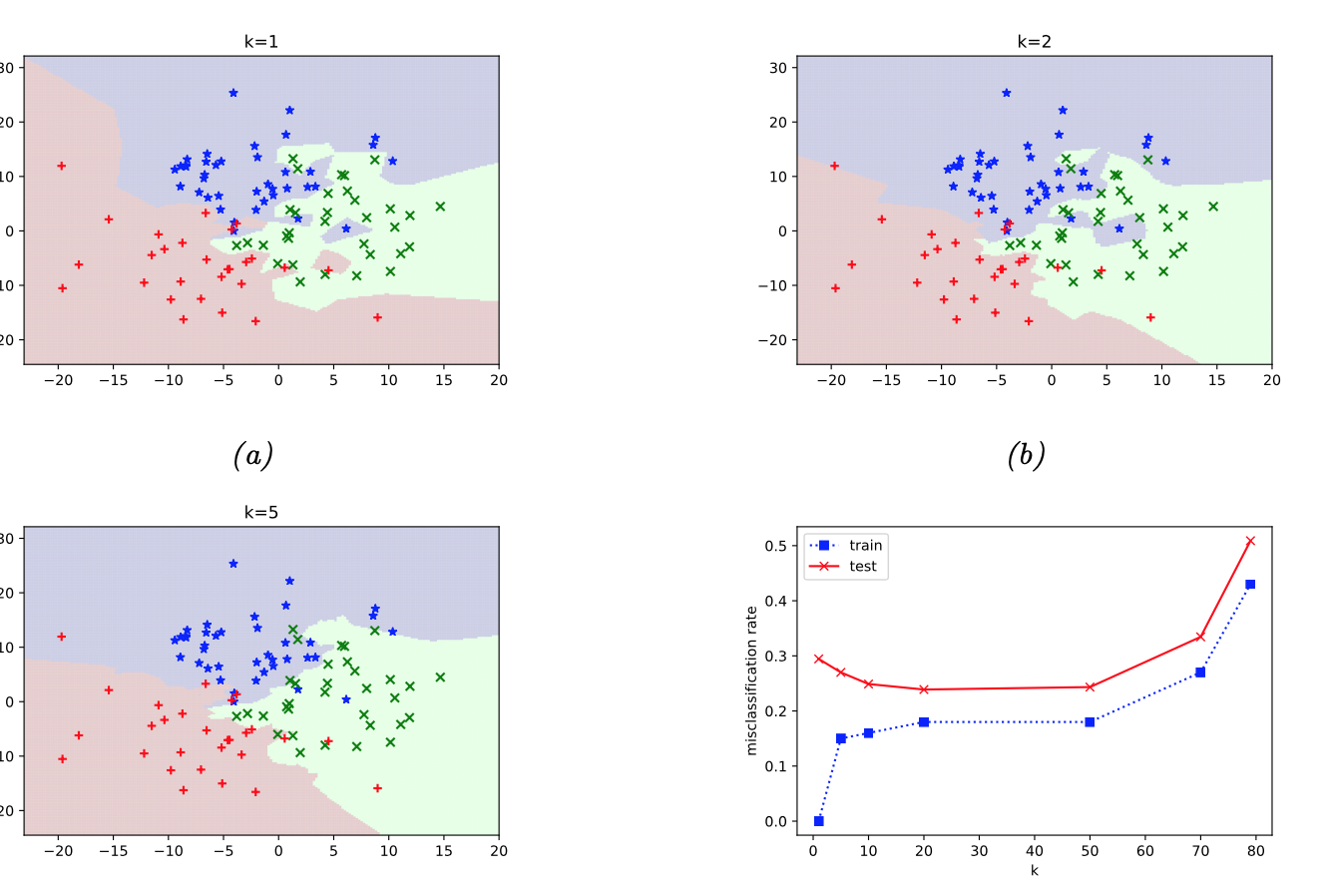
../_images/Murphy_16_2.png

Q. Look at the graph of train and test errors. For which values of \(k\) we can suspect overfitting?

Effective number of parameters of \(k\)-NN

It is equal to \(\frac n k\). To get an idea of why, note that if the neighborhoods were nonoverlapping, there would be \(\frac nk\) neighborhoods and we would fit one parameter (a mean) in each neighborhood ([Hastie et al., 2009], p. 14)

Curse of dimensionality#

https://www.researchgate.net/publication/347363976/figure/fig4/AS:970060722089985@1608291907488/Geometry-for-the-computation-of-the-volume-of-the-slice-We-ideally-slice-the-large-piece.png

Only red part of watermelon is useful, and watermelon rind is thrown away. Suppose that the watermelon is a ball of radius \(R\), and the length of the rind is \(10\%\) of \(R\).

This is how the curse of dimensionality works. In \(50\)-dimensional space there is almost nothing to eat in a watermelon.

../_images/333ad74bb4abf0bd41429f73138a7245c5c7e848677d6b3a9ed0e118ff02ed0c.svg

What are the consequenes of curse of the dimensionality for \(k\)-NN?

A common example from textbooks

Suppose we apply a \(k\)-NN classifier to data where the inputs are uniformly distributed in the \(d\)-dimensional unit cube. Suppose we estimate the density of class labels around a test point \(\boldsymbol x\) by “growing” a hyper-cube around \(\boldsymbol x\) until it contains a desired fraction \(p\) of the data points. The expected edge length of this cube will be \(e_d(p)=p^{\frac 1d}\) (see [Murphy, 2022], p. 530-531). For example, if \(d=10\) and we want to capture \(1\%\) of neighbours, we need extend the cube \(e_{10}(0.01) \approx 0.63\) along each dimension around \(\boldsymbol x\).

../_images/d2431586e5190fb9035c58c1e47b951e90f618aa480feeaa80bee6dfdb73e21d.svg

TODO

  • Make the last plot interactive

  • Apply k-NN to some real datasets

  • Add a plot and quiz on manual calculations with nearest neighbors