Matrices

Табличный способ хранения данных чрезвычайно широко распространён, и если эти данные числовые, то с математической точки зрения они образуют матрицу — двумерный массив из чисел. Для эффективной обработки и анализа таких данных, а также обучения моделей машинного обучения на них, важно хорошо ориентироваться в матричных операциях и разложениях и их свойствах.

Матрицы принято обозначать заглавными жирными буквами: \(\boldsymbol A\), \(\boldsymbol B\), \(\boldsymbol C\), \(\boldsymbol X\), \(\boldsymbol Y\) и т.п. Множество матриц, имеющих \(m\) строк и \(n\) столбцов обозначается через \(\mathbb R^{m\times n}\). Элемент \(i\)-й строки и \(j\)-го столбца матрицы \(\boldsymbol A \in \mathbb R^{m\times n}\) будем обозначать \(A_{ij}\). Допустимо также обозначение \(a_{ij}\), особенно когда дело доходит до подробной записи

\[\begin{split} \boldsymbol A = \begin{pmatrix} a_{11} & a_{12} & \dots & a_{1n} \\ a_{21} & a_{22} & \dots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \dots & a_{mn} \\ \end{pmatrix}. \end{split}\]

Эту же матрицу можно представить как набор строк или столбцов:

\[\begin{split} \boldsymbol A = \begin{pmatrix} \boldsymbol b_1^\top \\ \boldsymbol b_2^\top \\ \vdots\\ \boldsymbol b_m^\top \\ \end{pmatrix} = [\boldsymbol c_1 \boldsymbol c_2 \dots \boldsymbol c_n], \quad \boldsymbol b_i = \begin{pmatrix} a_{i1} \\ a_{i2} \\ \vdots \\ a_{in} \end{pmatrix}, \quad \boldsymbol c_j = \begin{pmatrix} a_{1j} \\ a_{2j} \\ \vdots \\ a_{mj} \end{pmatrix} \end{split}\]

Если \(m=n\), то матрица \(\boldsymbol A\) называется квадратной, в противном случае — прямоугольной. Вектор \(\boldsymbol x \in \mathbb R^n\) можно считать матрицей размера \(n\times 1\) (столбец) или \(1\times n\) (строка).

Транспонированная матрица \(\boldsymbol A^\top \in \mathbb R^{n\times m}\) в качестве строк содержит столбцы матрицы \(\boldsymbol A\): \(A^\top_{ij} = A_{ji}\). В частности, вектор-столбец получается транспонированием из вектора-строки, и наоборот, чем и объясняется обозначение \(\boldsymbol x^\top\) для векторов-строк.

np.array can handle multidimenstional arrays including matrices. For example, let’s generate a random matrix of shape \(2\times 3\)

import numpy as np
A = np.random.rand(2, 3)
A

array([[0.08728969, 0.54601015, 0.72351181],
       [0.96028496, 0.03162472, 0.2270256 ]])

For transposing use attribute .T:

A.T

array([[0.08728969, 0.96028496],
       [0.54601015, 0.03162472],
       [0.72351181, 0.2270256 ]])

Square matrices

Квадратные матрицы \(\boldsymbol A \in \mathbb R^{n\times n}\) имеют одинаковое количество строк и столцов. Такие матрицы представляют особый интерес как в теории, так и на практике.

У квадратной матрицы есть две диагонали: главная и побочная.

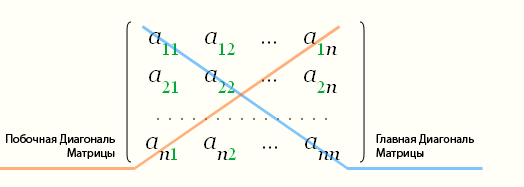
Сумма элементов главной диагонали называется следом матрицы: \(\mathrm{tr}(\boldsymbol A) = \sum\limits_{i=1}^n a_{ii}\).

Перечислим самые распространённые классы квадратных матриц.

1. Единичная матрица. Такая матрица содержит единицы на главной диагонали и нули вне неё; обозначается \(\boldsymbol I\) или \(\boldsymbol I_n\), если нужно подчеркнуть её размер:

   \[\begin{split} \boldsymbol I_2 = \begin{pmatrix} 1 & 0 \\ 0 & 1 \\ \end{pmatrix}, \quad \boldsymbol I_3 = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix}, \quad \boldsymbol I_n = \begin{pmatrix} 1 & 0 & \dots & 0 \\ 0 & 1 & \dots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 &\dots & 1 \\ \end{pmatrix}. \end{split}\]

2. Диагональная матрица. Все ненулевые элементы диагональной матрицы находятся на главной диагонали:

   \[\begin{split} \boldsymbol \Lambda = \mathrm{diag}\{\lambda_1, \lambda_2, \ldots, \lambda_n\} = \begin{pmatrix} \lambda_1 & 0 & \dots & 0 \\ 0 & \lambda_2 & \dots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \dots & \lambda_n \\ \end{pmatrix}. \end{split}\]

   Единичная матрица является частным случаем диагональной:

   \[ \boldsymbol I = \mathrm{diag}\{1, 1, \dots, 1\}. \]

3. Матрица перестановки. Такая матрица состоит из нулей и единиц, и содержит ровно одну единицу в каждой строке и в каждом столбце. Любая матрица перестановки получается некоторой перестановкой строк/столбцов единичной матрицы. Существует \(n!\) различных матриц перестановок размера \(n\times n\). Например, ниже перечислены все \(3!=6\) матрицы перестановок размера \(3\times3\):

   \[\begin{split} \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix}, \quad \begin{pmatrix} 1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \\ \end{pmatrix}, \quad \begin{pmatrix} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix}, \end{split}\]
   \[\begin{split} \begin{pmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \\ \end{pmatrix}, \quad \begin{pmatrix} 0 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ \end{pmatrix}, \quad \begin{pmatrix} 0 & 0 & 1 \\ 0 & 1 & 0 \\ 1 & 0 & 0 \\ \end{pmatrix}. \end{split}\]

4. Треугольные матрицы. У верхней треугольной матрицы \(\boldsymbol U\) все элементы ниже главной диагонали равны нулю: \(U_{ij} = 0\) при \(i > j\),

   \[\begin{split} \boldsymbol U = \begin{pmatrix} u_1 & * & * & \dots & * \\ 0 & u_2 & * & \dots & * \\ 0 & 0 & u_3 & \dots & * \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \dots & u_n \\ \end{pmatrix}. \end{split}\]

   У нижней треугольной матрицы \(\boldsymbol L\), наоборот, все элементы выше главной диагонали равны нулю: \(L_{ij} = 0\) при \(i < j\),

   \[\begin{split} \boldsymbol L = \begin{pmatrix} \ell_1 & 0 & 0 & \dots & 0 \\ * & \ell_2 & 0 & \dots & 0 \\ * & * & \ell_3 & \dots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ * & * & * & \dots & \ell_n \\ \end{pmatrix}. \end{split}\]

   Матрица \(\boldsymbol U\) верхняя треугольная тогда и только тогда, когда матрица \(\boldsymbol U^\top\) нижняя треугольная.

5. Симметричные матрицы. Квадратная матрица \(\boldsymbol A\) называется

   • симметричной, если \(\boldsymbol A^\top = \boldsymbol A\);

   • кососимметричной, если \(\boldsymbol A^\top = -\boldsymbol A\).

   На главной диагонали кососимметричной матрицы всегда находятся нули. Всякая квадратная матрица \(\boldsymbol A\) может быть единственным образом представлена в виде суммы симметричной и кососимметричной матриц:

   \[ \boldsymbol A = \frac{\boldsymbol A + \boldsymbol A^\top}2 + \frac{\boldsymbol A - \boldsymbol A^\top}2. \]

6. Ортогональная матрица. Квадратная матрица \(\boldsymbol Q = [\boldsymbol q_1, \ldots, \boldsymbol q_n]\) ортогональная, если её столбцы образуют ортонормированную систему, т. е. \(\langle \boldsymbol q_i, \boldsymbol q_j\rangle = \delta_{ij}\), где \(\delta_{ij}\) — символ Кронекера{:target=”_blank”}.

   Любая матрица перестановки является ортогональной. Также ортогональна, к примеру, матрица поворота на угол \(\theta\)

   (29)\[\begin{split}\boldsymbol Q = \begin{pmatrix} \cos \theta & -\sin\theta \\ \sin \theta & \cos\theta \\ \end{pmatrix}.\end{split}\]

Identity matrix in NumPy is created by np.eye:

I = np.eye(4, dtype=np.int32)
I

array([[1, 0, 0, 0],
       [0, 1, 0, 0],
       [0, 0, 1, 0],
       [0, 0, 0, 1]], dtype=int32)

np.diag can either create a diagonal matrix or extract the main diagonal of a matrix. Here we create a diagonal matrix:

D = np.diag([1, 2, 3])
D

array([[1, 0, 0],
       [0, 2, 0],
       [0, 0, 3]])

A = np.random.normal(size=(3, 3))
A

array([[-0.44717254,  1.4078295 , -0.6438964 ],
       [ 0.30502598,  1.0711746 ,  1.15591706],
       [ 1.51407551,  1.83549146, -1.7051814 ]])

And here the extraction of the main diagonal happens:

np.diag(A)

array([-0.44717254,  1.0711746 , -1.7051814 ])

Matrix operations

Перечислим поэлементные операции с матрицами. Пусть матрицы \(\boldsymbol A, \boldsymbol B \in \mathbb R^{m\times n}\), \(\alpha \in \mathbb R\), \(1 \leqslant i \leqslant m\), \(1\leqslant j \leqslant n\).

• Сложение матриц:

\[ \boldsymbol С = \boldsymbol A + \boldsymbol B \iff C_{ij} = A_{ij} + B_{ij}. \]

• Умножение матрицы на скаляр:

\[ \boldsymbol B = \alpha \boldsymbol A \iff B_{ij} = \alpha A_{ij}. \]

• Поэлементное умножение (произведение Адамара) и деление матриц:

  \[ \boldsymbol C = \boldsymbol A \odot \boldsymbol B \iff C_{ij} = A_{ij} B_{ij},\quad \boldsymbol D = \boldsymbol A \oslash \boldsymbol B \iff D_{ij} = \frac{A_{ij}}{B_{ij}} \]

  (последнее возможно, разумеется, только если все элементы матрицы \(\boldsymbol B\) не равны нулю). Стоит отметить, что под произведением матриц обычно понимают совсем иную операцию, нежели поэлементное умножение, и о ней предстоит отдельный разговор.

Первые два свойства указывают на то, что матрицы можно рассматривать как вектора особого вида. Можно даже пойти дальше и записать матрицу размера \(m\times n\) в виде одномерного массива длины \(mn\) (например, построчно), и получится вектор в чистом виде. Такая операция применяется, к примеру, в свёрточных нейронных сетях, когда на определённом этапе представленная матрицей или тензором картинка выпрямляется (flatten) в вектор для дальнейшего прохождения через один или несколько полносвязных слоёв.

Matrix operations in NumPy are quite natrural:

A = np.random.randint(-2, 3, size=(2, 3))
B = np.arange(1, 7).reshape(2, 3)
print(A)
print(B)

[[ 0 -2  0]
 [ 1  1 -1]]
[[1 2 3]
 [4 5 6]]

A + B

array([[1, 0, 3],
       [5, 6, 5]])

A - B

array([[-1, -4, -3],
       [-3, -4, -7]])

A * B

array([[ 0, -4,  0],
       [ 4,  5, -6]])

A / B

array([[ 0.        , -1.        ,  0.        ],
       [ 0.25      ,  0.2       , -0.16666667]])

Matrix-vector product

Чтобы матрицу \(\boldsymbol A\) можно было умножить на вектор \(\boldsymbol x\), число её столбцов должно совпадать с размерностью вектора \(\boldsymbol x\). Если \(\boldsymbol A \in \mathbb R^{m\times n}\), \(\boldsymbol x \in \mathbb R^n\), то \(\boldsymbol A\boldsymbol x = \boldsymbol b \in \mathbb R^m\); координаты вектора \(\boldsymbol b\) вычисляются по формуле

\[ b_i = \sum\limits_{j=1}^n A_{ij} x_j, \quad 1 \leqslant i \leqslant m. \]

По-другому можно сказать, что \(b_i = \boldsymbol a_i^\top \boldsymbol x\), где \(\boldsymbol a_i^\top\) — \(i\)-я строка матрицы \(\boldsymbol A\). Таким образом, для умножения матрицы на вектор требуется вычислить \(m\) скалярных произведений \(n\)-мерных векторов, поэтому сложность этих вычислений составляет \(O(mn)\). Если матрица \(\boldsymbol A\) квадратная размера \(n\times n\), то эта сложность равна \(O(n^2)\).

На матрично-векторное умножение можно взглянуть с другой стороны. А именно, если обозначить \(j\)-й столбец через \(\boldsymbol a_j\), то получается, что

\[ \boldsymbol b = \boldsymbol A\boldsymbol x = \sum\limits_{j=1}^n x_j \boldsymbol a_j. \]

Таким образом, вектор \(\boldsymbol b = \boldsymbol A\boldsymbol x\) является линейной комбинацией столбцов матрицы \(\boldsymbol A\) с координатами вектора \(\boldsymbol x\) в качестве коэффициентов.

Умножая матрицу на вектор-столбец, мы получаем снова вектор-столбец; умножение матрицы на вектор-строку записывают в обратном порядке:

\[ \boldsymbol y^\top \boldsymbol A = \boldsymbol c^\top,\quad \boldsymbol y \in \mathbb R^m, \quad \boldsymbol A \in \mathbb R^{m\times n}, \quad \boldsymbol c \in \mathbb R^n, \quad c_j = \sum\limits_{i=1}^m y_i A_{ij}. \]

Результат такого умножения представляет собой линейную комбинацию строк матрицы \(\boldsymbol A\): \(\boldsymbol c^\top = \sum\limits_{i=1}^m y_i \boldsymbol a_i^\top\).

Заметим, что матрицу \(\boldsymbol A\) размера \(1 \times n\) можно представить в виде вектора-строки \(\boldsymbol a^\top\). С другой стороны, согласно определению результат её умножения на вектор \(\boldsymbol x \in \mathbb R^n\) равен числу

\[ \boldsymbol A \boldsymbol x = \boldsymbol a^\top \boldsymbol x = \sum\limits_{j=1}^n a_j x_j, \]

а это в точности скалярное произведение \(\langle \boldsymbol a, \boldsymbol x\rangle\). Отсюда и проистекает его весьма популярное обозначение через матрично-векторное произведение \(\boldsymbol a^\top \boldsymbol x\), которым мы также будем активно пользоваться в дальнейшем.

Since matrix times vector operation is quite similar to inner products, the Python syntax is the same as here:

A = np.arange(9).reshape(3, -1)
b = np.array([2, 1, -1])
A

array([[0, 1, 2],
       [3, 4, 5],
       [6, 7, 8]])

A.dot(b), np.dot(A, b), A @ b

(array([-1,  5, 11]), array([-1,  5, 11]), array([-1,  5, 11]))

Matrix product

Матрицу \(\boldsymbol A\) можно умножить на матрицу \(\boldsymbol B\), если количество столбцов матрицы \(\boldsymbol A\) равно числу строк матрицы \(\boldsymbol B\). А именно, произведением матриц \(\boldsymbol A \in\mathbb R^{m\times n}\) и \(\boldsymbol B \in\mathbb R^{n\times p}\) является матрица \(\boldsymbol C = \boldsymbol A \boldsymbol B \in\mathbb R^{m\times p}\), каждый элемент которой равен

\[ C_{ik} = \sum\limits_{j=1}^n A_{ij}B_{jk},\quad 1\leqslant i \leqslant m, \quad 1\leqslant k \leqslant p. \]

Элементы матрицы \(\boldsymbol C\) можно записать в виде \(C_{ik} = \boldsymbol a_i^\top \boldsymbol b_k\), где \(\boldsymbol a_i^\top\) — строки матрицы \(\boldsymbol A\), а \(\boldsymbol b_k\) — столбцы матрицы \(\boldsymbol B\). Вычисление каждого элемента \(C_{ik}\) требует \(O(n)\) арифметических операций, поэтому общая сложность подсчёта произведения матриц составляет \(O(mnp)\). Если все матрицы квадратные размера \(n\times n\), то сложность будет \(O(n^3)\).

А быстрее можно?

Алгоритм Штрассена позволяет перемножать квадратные матрицы чуть быстрее, а именно за \(O(n^{\log_2 7})\), что примерно составляет \(O(n^{2.81})\). Алгоритм Штрассена был разработан ещё в 1969 году, и с тех пор было предложено множество алгоритмов с лучшей асимптотикой. Подробнее про эту гонку можно почитать в этой статье, где текущая SoTA указана как \(O(n^{2.3728596})\). Математики не оставляют надежд добиться асимптотики \(O(n^2)\) или хотя бы \(O(n^{2+\varepsilon})\) для любого сколь угодно малого \(\varepsilon > 0\), однако, все эти изыскания носят сугубо теоретический характер из-за гигантских констант в O-большом и сложности реализации подобных алгоритмов.

Впрочем, сегодня новые алгоритмы перемножения матриц придумывают не только математики, но и нейронные сети. Например, компания DeepMind с помощью глубокого обучения подкрепления разработала алгоритм AlphaTensor способный перемножать матрицы размера \(5\times 5\) эффективнее, чем алгоритм Штрассена (\(76\) умножений против \(80\)).

Произведение матриц \(\boldsymbol A \boldsymbol B\) можно представить также в виде набора столбцов, получающихся умножением матрицы \(\boldsymbol A\) на столбцы матрицы \(\boldsymbol B\): если \(\boldsymbol B = [\boldsymbol b_1 \ldots \boldsymbol b_p]\), то

\[ \boldsymbol A \boldsymbol B = [\boldsymbol A\boldsymbol b_1 \ldots \boldsymbol A\boldsymbol b_p]. \]

Или же можно строки матрицы \(\boldsymbol A\) умножать на матрицу \(\boldsymbol B\): если

\[\begin{split} \boldsymbol A = \begin{pmatrix} \boldsymbol a_1^\top \\ \boldsymbol a_2^\top \\ \vdots\\ \boldsymbol a_m^\top \\ \end{pmatrix}, \text{ то } \boldsymbol A \boldsymbol B = \begin{pmatrix} \boldsymbol a_1^\top \boldsymbol B \\ \boldsymbol a_2^\top \boldsymbol B \\ \vdots\\ \boldsymbol a_m^\top \boldsymbol B \\ \end{pmatrix}. \end{split}\]

Свойства матричного умножения (предполагается, что размеры всех матриц согласованы)

1. \((\boldsymbol{AB})\boldsymbol{C} = \boldsymbol{A}(\boldsymbol{BC})\) (ассоциативность)

2. \((\boldsymbol A + \boldsymbol B)\boldsymbol{C} = \boldsymbol{AC} + \boldsymbol{BC}\), \(\boldsymbol{C}(\boldsymbol A + \boldsymbol B) = \boldsymbol{CA} + \boldsymbol{CB}\) (дистрибутивность)

3. \((\boldsymbol{AB})^\top = \boldsymbol B^\top \boldsymbol A^\top\)

4. \(\mathrm{tr}(\boldsymbol{AB}) = \mathrm{tr}(\boldsymbol{BA})\)

Последнее свойство обобщается до равенства \(\mathrm{tr}(\boldsymbol{ABС}) = \mathrm{tr}(\boldsymbol{СAB})\), которое справедливо для любого числа сомножителей с согласованными размерами. Это так называемое циклическое свойство следа матрицы.

Несколько дополнительных свойств для квадратных матриц:

• \(\boldsymbol{AI} = \boldsymbol{IA} = \boldsymbol A\);

• если \(\boldsymbol P\) — матрица перестановки, то матрица \(\boldsymbol{PA}\) получается из матрицы \(\boldsymbol A\) перестановкой строк, а матрица \(\boldsymbol{AP}\) — перестановкой столбцов;

• произведение двух верхних (нижних) треугольных матриц тоже верхняя (нижняя) треугольная матрица;

• если матрица \(\boldsymbol Q\) ортогональна, то \(\boldsymbol{QQ}^\top = \boldsymbol Q^\top \boldsymbol Q = \boldsymbol I\).

А вот коммутировать квадратные матрицы не обязаны: в общем случае \(\boldsymbol{AB} \ne \boldsymbol{BA}\) (поищите контрпример среди матриц размера \(2\times 2\)).

Квадратные матрицы можно возводить в натуральную степень так же, как и обычные числа. Вот, например, индуктивное определение степени матрицы:

\[ \boldsymbol A^n = \boldsymbol A^{n-1} \boldsymbol A, \quad n\in\mathbb N,\quad \boldsymbol A^0 = \boldsymbol I. \]

Справедливы равенства

\[ \boldsymbol A^{m+n} = \boldsymbol A^m\boldsymbol A^n,\quad \boldsymbol A^{mn} = \boldsymbol (\boldsymbol A^m)^n, \quad m, n \in \mathbb N. \]

Можно даже пойти дальше, и определить взятие экспоненты или синуса от матрицы через ряд Тейлора:

\[ \exp(\boldsymbol A) = \sum\limits_{n=0}^\infty \frac{\boldsymbol A^n}{n!},\quad \sin(\boldsymbol A) = \sum\limits_{n=0}^\infty (-1)^n\frac{\boldsymbol A^{2n+1}}{(2n+1)!} \]

(можно доказать, что эти ряды сходятся).

Замечание. В машинном (и особенно глубинном) обучении часто берут числовую функцию от матрицы, например \(\log(\boldsymbol A)\), \(\tanh(\boldsymbol A)\) или \(\sigma(\boldsymbol A)\), где \(\sigma(x) = \frac 1{1+e^{-x}}\) — сигмоида. Такая запись почти наверное подразумевает поэлементное применение функции к каждой ячейке матрицы \(\boldsymbol A\), а вовсе не матричные ряды! Тем более что матрицы в машинном обучении чаще всего прямоугольные, а для них нельзя определить ни степень, ни ряд.

Matrix product in NumPy is similar to that of vectors:

A = np.array([[1, 2, 3], [4, 5, 6]])
B = np.arange(12).reshape(3, 4)
print(A.shape, B.shape)

(2, 3) (3, 4)

A.dot(B)

array([[ 32,  38,  44,  50],
       [ 68,  83,  98, 113]])

Exponent is elementwise:

np.exp(B)

array([[1.00000000e+00, 2.71828183e+00, 7.38905610e+00, 2.00855369e+01],
       [5.45981500e+01, 1.48413159e+02, 4.03428793e+02, 1.09663316e+03],
       [2.98095799e+03, 8.10308393e+03, 2.20264658e+04, 5.98741417e+04]])

One-rank matrix

Одноранговая матрица задаётся произведением столбца на строку: \(\boldsymbol A = \boldsymbol {uv}^\top\), \(\boldsymbol u \in \mathbb R^m\), \(\boldsymbol v \in \mathbb R^n\). Элементы этой прямоугольной матрицы равны \(A_{ij} = u_i v_j\), а все её строки/столбцы пропорциональны. Отметим также, что если \(m=n\), то

\[ \mathrm{tr}(\boldsymbol {uv}^\top) = \sum\limits_{i=1}^n u_i v_i = \boldsymbol v^\top \boldsymbol u = \mathrm{tr}(\boldsymbol v^\top \boldsymbol u). \]

Произведение матриц \(\boldsymbol A \in\mathbb R^{m\times n}\) и \(\boldsymbol B \in\mathbb R^{n\times p}\) можно записать в виде суммы одноранговых матриц:

\[\begin{split} \boldsymbol {AB} = [\boldsymbol a_1, \ldots, \boldsymbol a_n] \begin{pmatrix} \boldsymbol b_1^\top \\ \boldsymbol b_2^\top \\ \vdots\\ \boldsymbol b_n^\top \\ \end{pmatrix} = \sum\limits_{j=1}^n \boldsymbol a_j \boldsymbol b_j^\top. \end{split}\]

В англоязычной литературе умножение столбца на строку \(\boldsymbol {uv}^\top\) называется outer product («внешнее произведение»), по аналогии со скалярным произведением \(\boldsymbol u^\top\boldsymbol v\), называемым inner product («внутреннее произведение»).

Block matrices

Блочная матрица имеет вид

\[\begin{split} \begin{pmatrix} \boldsymbol A & \boldsymbol B \\ \boldsymbol C & \boldsymbol D \end{pmatrix} = \left(\begin{array}{@{}c|c@{}} \begin{matrix} a_{11} & \dots & a_{1m} \\ \vdots & \ddots & \vdots \\ a_{k1} & \dots & a_{km} \end{matrix} & \begin{matrix} b_{11} & \dots & b_{1n} \\ \vdots & \ddots & \vdots \\ b_{k1} & \dots & b_{kn} \end{matrix} \\ \hline \begin{matrix} c_{11} & \dots & c_{1m} \\ \vdots & \ddots & \vdots \\ c_{\ell 1} & \dots & c_{\ell m} \end{matrix} & \begin{matrix} d_{11} & \dots & d_{1n} \\ \vdots & \ddots & \vdots \\ d_{\ell 1} & \dots & d_{\ell n} \end{matrix} \end{array}\right). \end{split}\]

Контрольный вопрос. Каков будет результат транспонирования блочной матрицы

\[\begin{split} \begin{pmatrix} \boldsymbol A & \boldsymbol B \\ \boldsymbol C & \boldsymbol D \end{pmatrix}, \end{split}\]

где \(\boldsymbol A \in \mathbb R^{k\times m}\), \(\boldsymbol B \in \mathbb R^{k\times n}\), \(\boldsymbol C \in \mathbb R^{\ell\times m}\), \(\boldsymbol D \in \mathbb R^{\ell\times n}\)?

Ответ

Блоки $\boldsymbol B$ и $\boldsymbol C$ надо переставить, и не забыть ещё транспонировать каждый блок:

\[\begin{split} \begin{pmatrix} \boldsymbol A^\top & \boldsymbol C^\top \\ \boldsymbol B^\top & \boldsymbol D^\top \end{pmatrix}. \end{split}\]

Блочные матрицы могут иметь произвольное число матричных блоков по каждому измерению. Интересно, что перемножать блочные матрицы можно по тем же правилам, что и матрицы из чисел, например

\[\begin{split} \begin{pmatrix} \boldsymbol A_{11} & \boldsymbol A_{12} \\ \boldsymbol A_{21} & \boldsymbol A_{22} \end{pmatrix} \begin{pmatrix} \boldsymbol B_1 \\ \boldsymbol B_2 \end{pmatrix} = \begin{pmatrix} \boldsymbol A_{11} \boldsymbol B_1 + \boldsymbol A_{12} \boldsymbol B_2 \\ \boldsymbol A_{21} \boldsymbol B_1 + \boldsymbol A_{22} \boldsymbol B_2 \end{pmatrix} \end{split}\]

(при условии, что размеры матриц позволяют корректно произвести все матричные умножения).

Exercises

1. Prove that the rotation matrix (29) is orthogonal.

2. Prove that any reflection matrix \(\boldsymbol I - 2\boldsymbol u \boldsymbol u^\top\), \(\boldsymbol u \in\mathbb R^n\), \(\Vert \boldsymbol u \Vert_2 = 1\), is orthogonal.

3. Prove that \(\mathrm{tr}(\boldsymbol{AB}) = \mathrm{tr}(\boldsymbol{BA})\).

4. Let \(\boldsymbol A\) and \(\boldsymbol B\) be two symmetric matrices of the same shape. Is their product is necessarily symmetric?